Proyección en OpenGL

Ortogonal.

El tipo de proyección que hemos utilizado hasta ahora es una proyección ortogonal. Una proyección ortogonal define un volumen de la vista de tipo paralelepipédico tal y como se muestra en la siguiente figura. La principal característica de esta proyección es que el tamaño de los objetos es independiente de la distancia a la que estén del observador, por ejemplo, dos cilindros del mismo tamaño, uno a cinco unidades y el otro a diez unidades de distancia del observador se proyectarán con el mismo tamaño.

Para definir una proyección ortogonal en OpenGL hay que dar los siguiente pasos:

Codigo Ejemplo 

glMatrix(GL_PROJECTION); /* Voy a manejar la matriz de proyección */

glLoadIdentity(); /* Cargo inicialmente la identidad */

/* Y ahora defino la proyección ortogonal */

void glOrtho(izquierda, derecha, abajo, arriba, cerca, lejos);

Perspectiva.

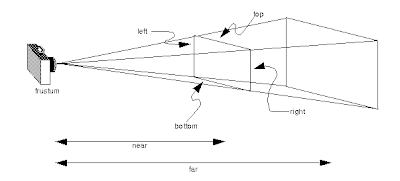
La proyección ortogonal no da sensación de profundidad porque el tamaño de los objetos no depende de su distancia al observador. Para conseguir este efecto  necesitamos definir una proyección perspectiva. Esta proyección define un volumen de la vista que es una prisma truncado de base rectangular, como el de la siguiente figura:

a función OpenGL que establece este tipo de perspectiva es: Ejemplo void glFrustum(izquierda, derecha, abajo, arriba, cerca, lejos); este modo de definir la proyección perspectiva no es demasiado intuitivo, es más sencillo establecerla con un esquema como el que se muestra en la siguiente figura: y la función OpenGL que la establece es: Ejemplo void gluPerspective(fovy, aspecto, cerca, lejos); donde fovy es el ángulo de apertura del objetivo de la cámara, en grados  y aspecto es la relación ancho/alto de la base de la pirámide.  Transformaciones Geométricas Traslación La traslación es una transformación puntual por la cual a todo  punto A del plano le corresponde otro punto A' también del  plano de forma que . Siendo  el vector que define la traslación. Rotación. La rotación es un movimiento angular de cada uno de los puntos a partir de un punto  que es el centro de giro. Para este movimiento es necesario dar un ángulo y el punto centro de giro. Escalacion. Resumen Enlace. LA PILA DE MATRICES En la función display() se encuentran las llamadas a dos funciones de matrices que todavía no han sido comentadas. Se trata de glPushMatrix() y glPopMatrix(). Para comprender su funcionamiento, primero se va a experimentar que es lo que ocurre cuando no están dichas llamadas. Para ello se comentan en la función display()  ambas llamadas: void display(void) { ... // glPushMatrix(); ... glTranslatef(0.0, 0.0, .5); ... // glPopMatrix(); glutSwapBuffers(); } DIBUJANDO UN RASTRO Una característica de Logo es que la tortuga al avanzar va dibujando el camino por  el que ha pasado. Hasta ahora la aplicación va transformando las coordenadas del objeto  para situarlo en la nueva posición según las instrucciones introducidas pero no muestra  la ruta seguida. Para mostrar la ruta es necesario almacenar los puntos por los que pasa la tortuga. El rastro consistirá en una línea que una estos puntos. Necesitaremos realizar tres operaciones: calcular la coordendas donde se encuentra la tortuga, almacenar dicha coordenada y dibujar el rastro. Para almacenar los puntos se utiliza una variable para indicar el número de puntos y tres vectores para las coordenadas x, y, z. int np = 0; float px [10000]; float py [10000]; float pz [10000];